1. Préliminaires
Disposant de la représentation d'une fonction f(x), sous la forme d'un polynôme d'interpolation de degré N fN(x) , on peut évaluer l'intégrale de f(x) sur [-1;1] en intégrant fN(x).Le polynôme d'interpolation fN(x), développé sur les polynômes de Tchebychev, est:
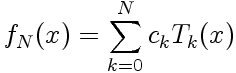
|
2. Intégration
L'intégration de fN(x) se résume à une somme (pondérée des coefficients ck) des N premiers polynômes de Tchebychev Tk(x).Or, la valeur de l'intégrale sur [-1;1] des Tk(x) est bien connue:
![Intégrale, sur [-1;1], des polynômes de Tchebychev Intégrale, sur [-1;1], des polynômes de Tchebychev](../Tchebychev/poly_tcheby_integrale.png)
|
![Expression de l'intégrale, sur [-1;1], du polynôme d'interpolation Expression de l'intégrale, sur [-1;1], du polynôme d'interpolation](../Tchebychev/poly_interp_tcheby_integrale.png)
|
3. Aspects pratiques
Comme toujours, lorsqu'il s'agit des polynômes de Tchebychev, il est impératif de travailler sur l'intervalle [-1;1].Lorsqu'on s'intéresse à un autre domaine, par exemple [z A;z B], il faut se ramener à [-1;1] par un changement de variable. En clair, si z est dans [z A;z B], on passe à x dans [-1;1] par le changement de variable z = R.x + K, avec R = (z B-z A)/2 et K = (z B+z A)/2.
A ce propos, ne pas oublier de multiplier le resultat de l'integration (par rapport à x) sur [-1;1], par R pour obtenir la valeur de l'intégrale (par rapport à z) sur [z A;z B].