1. Le polynôme d'interpolation de Tchebychev

Connaissant les (N+1) valeurs nodales d'une fonction f(x) aux points de collocation de Gauss, Gauss-Lobatto ou Gauss-Radau, on peut construire le polynôme d'interpolation (de degré N) f_N(x): Où les coefficients spectraux c_k sont complètement déterminés (voir la page à ce sujet).

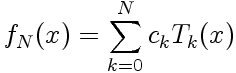
Connaissant les c_k, il est aisé de calculer f_N(x) en n'importe quel x, par application de la formule ci-dessus; calcul qui peut en outre être optimisé en tenant compte des expressions et de la relation de recurrence entre les polynômes de Tchebychev: Les termes de la série se calculant dans l'ordre ascendant et en peu d'opérations.

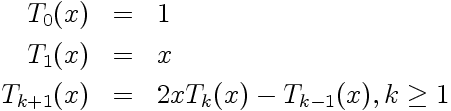
2. Convergence de l'approximation

Que le polynôme d'interpolation f_N(x) soit basé sur les points de collocation de Gauss, Gauss-Radau ou Gauss-Lobatto, il y a convergence exponentielle de f_N(x) vers f(x).

2.1 Exemple

N.B.: Cet exemple est également traité du point de vue de l'interpolation via les polynômes de Lagrange sur des points équidistants
Interpolation, sur l'intervalle [-1;1], de la fonction suivante:
A l'aide de (N+1) points de Gauss, on obtient des polynômes d'interpolation de degré N. Les écarts relatifs entre ces polynômes d'interpolation et f(x), pour N = 7, 10, 15 et 20, sont:

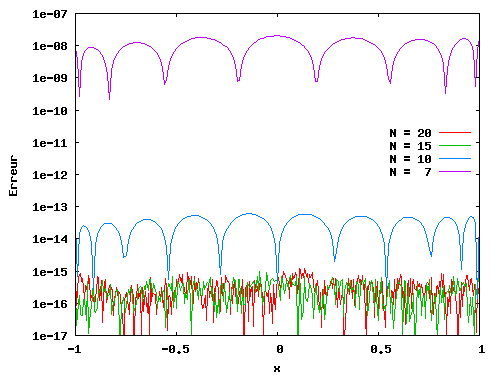
Ce qui illustre bien les propriés suivantes:

• La convergence extrêmement rapide du polynôme d'interpolation vers la fonction.
• L'excellente uniformité, à N donné, de l'écart à la solution sur tout l'intervalle d'interpolation.
• L'absence de dégénérescence de l'approximation avec la monté en degré du polynôme d'interpolation.
  Pour l'exemple ci-dessus, on voit bien que pour N=15, l'écart à la solution est déjà de l'ordre de l'epsilon machine et que cela reste le cas pour N=20.

Tous les commentaires ci-dessus résultent du (bon) choix des points de collocation, indépendement du fait de considérer le polynôme d'interpolation via les polynômes de Tchebychev.

2.2 Convergence des coefficients spectraux

Passons à présent à ce qui fait tout l'intérêt de l'approche qui consiste à considérer le développement du polynôme d'interpolation en terme d'une série des N premiers polynômes de Tchebychev T_k(x) (respectivement pondérés par les coefficients spectraux c_k).
En poursuivant l'approche par l'exemple ci-dessus, étudions l'évolution de l'amplitude des coefficients spectraux en fonction du degré du polynôme d'interpolation.
L'amplitude des coefficients spectraux c_k, pour N=3, 7, 10, 15 et 20 est:

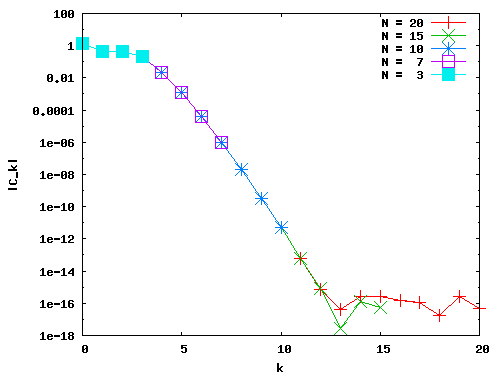
Ce qui illustre à merveille les comportements suivants:

• La convergence exponentielle de l'approximation (jusqu'ici évoqué sans justifications).
  Pour l'exemple ci-dessus elle apparait (c.-à-d.: elle se traduit par l'évolution, proportionnelle à exp(-k), de l'enveloppe des coefficients spectraux c_k) dès N = 5.
• La saturation des coefficients excédentaires autour de l'epsilon machine, une fois ce plateau atteint.
• La bonne convergence des coefficients, une fois ceux-ci inclus dans le développement, vers une valeur asymptotique.

3. Aspects pratiques et autres commentaires

La (grande) majorité du temps, on ne dispose pas de la fonction f(x) que l'on cherche à interpoler, mais seulement d'un jeu de valeurs prise par celle-ci aux points de collocation. Il est alors impossible d'évaluer formelement l'erreur comise lors d'une procédure d'interpolation.
A ce stade, il est vivement conseillé de prendre le temps de jeter un oeil au spectre des coefficients c_k; d'une part pour se faire une idée de la qualité de la représentation du signal, et d'autre part par ce qu'il est souvent observé que, une fois le régime de convergence exponentiel atteint, l'amplitude du coefficient c_N (le dernier du développement) est un bon indicateur de l'ordre de grandeur de l'écart du polynôme d'interpolation à la fonction f(x).