Polynômes de Lagrange

1. En bref

Connaissant les valeurs y _i = f(x _i) aux points x _i , on construit un polynôme P(x) passant par ces points. Le polynôme d'interpolation P(x) peut ensuite servir, dans la limite où il approxime suffisament bien f(x), pour calculer la valeur de la fonction en n'importe quel x.

2. Formulation du polynôme de Lagrange

On peut, à l'aide de (n+1) points {x _i , y _i = f(x _i), i = 0, ... , n} contruire le polynôme d'interpolation de Lagrange P _n(x) de degré n:

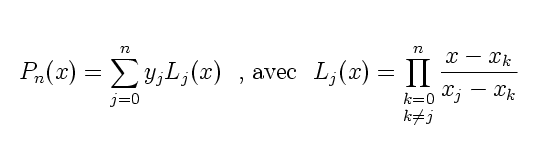
3. De l'interpolation sur des points équidistants et de la malédiction du phénomène de Runge

Autant le préciser d'emblée, représenter une fonction par un polynôme d'interpolation basé sur des points de collocation équirépartis n'est pas (et parfois de loin) la meilleure manière de faire.
Bien qu'intuitivement on puisse s'imaginer qu'employer un nombre de plus en plus grand de points de collocation (donc un polynôme d'interpolation d'ordre de plus en plus élevé) permette de représenter de plus en plus finement la fonction originelle, cette idée est fausse. En fait (résultat dû à Runge, vers le début du XXème sciècle), pour des degrés d'interpolation trop grands, le polynôme d'interpolation comportera des oscillations importantes au voisinage des bornes de l'intervalle d'interpolation. Ces oscillations, d'autant plus amples que le degré d'interpolation augmente, vouent invariablement toute tentative d'interpolation par un polynôme de degré trop élevé à un échec retentissant.

3.1 Un exemple rassurant

Au vu des avertissements du paragraphe précédent, on aurait tendance à croire qu'il est impératif de se cantonner à des polynômes d'interpolation de faible degré pour éviter le piège des oscillations de Runge. C'est vrai. Toutefois, la valeur suffisante de ce faible degré polynômiale au dela duquel l'interpolation vire à la catastrophe est très variable (et dépend évidemment de la fonction que l'on cherche à approcher).
Voici donc, pour tranquiliser les angoissés, un exemple rassurant:
Soit à interpoler la fonction suivante sur [-1;1]:
A l'aide de (n+1) points de collocation équirépartis sur [-1;1], on construit le polynôme d'interpolation de Lagrange de degré n.
Pour n = 3, 5 et 10, on obtient les polynômes suivants:

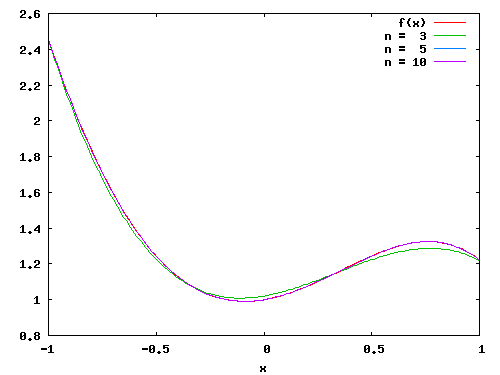
Où les courbes de f(x) et des polynômes n=5 et 10 sont confondues. Il est alors plus adéquat de visualiser les écarts relatifs entre ces polynômes et la fonction pour connaitre l'erreur comise par chacune de ces approximations. On obtient alors:

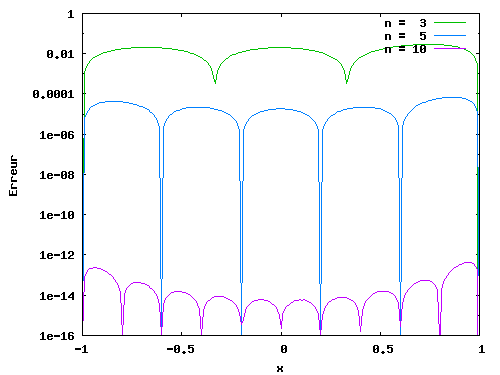
Graphique qui illustre clairement la bien meilleure précision du polynôme d'interpolation de degré 10.
Quid des oscillations de Runge? Pour l'instant, rien.
En poursuivant la monté en degré d'interpolation, on obtient les erreurs suivantes:

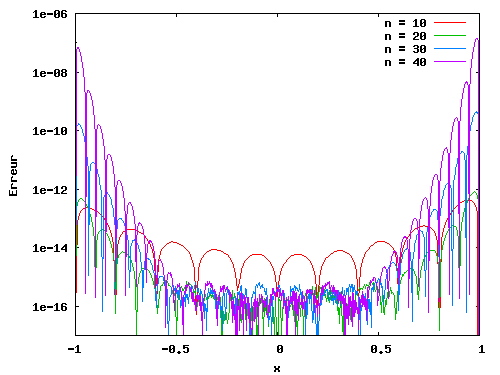
Où on constate la dégradation attendue (les fameuses oscillations de Runge sur les bords du domaine) pour n=30 puis 40.
Pour la fonction étudiée ici, le degré optimum du polynôme d'interpolation se situe autour de n=20.

3.2 Un exemple traumatisant

Passons maintenant à un cas bien moins sympathique, l'interpolation de f(x)=1/(1+x.x), sur [-5;5]. Pour un degré polynômial allant de 4 à 10, on obtient:

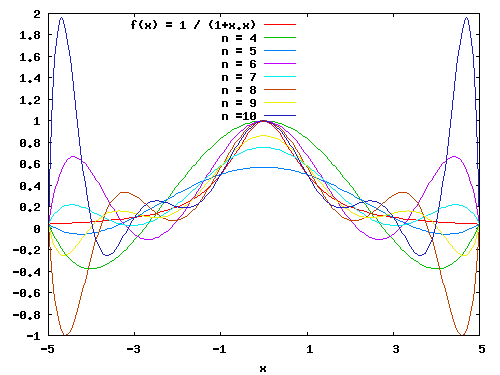
Il est clair qu'aucun de ces polynômes peut être qualifié de satisfaisant. Pire encore, on constate que dès que le degré polynômial devient plus grand que 6, les oscillations de Runge sont belle et bien présentes (et d'amplitude croissante avec n).
Si on passe outre et que l'on poursuit néanmoins la montée en degré polynômial, on obtient des erreurs d'interpolation de la forme:
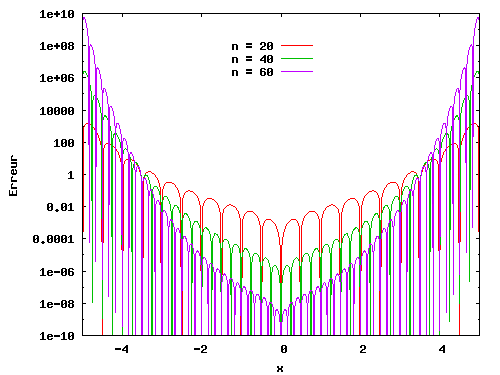
Sans commentaire..., si ce n'est que, en dépis des oscillations de plus en plus catastrophiques sur les bords du domaine, il y a malgré tout convergence du polynôme vers la fonction au centre de l'intervalle.

3.3 Récapitulatif et commentaires subsidiaires

L'apparition des oscillations de Runge est inévitable. Mais comme le montrent les deux exemples ci-dessus, tout dépend de la fonction que l'on cherche à représenter. Lorsque celle-ci est connue, il n'est pas difficile de vérifier la pertinence du degré polynômial employé. Lorsqu'il s'agit d'interpoler sur un jeu de valeurs numériques (résultant de mesures où de calculs) dont la fonction génératrice n'est pas connue, évaluer le bon degré polynômial ou l'erreur commise est généralement impossible...
Dernier petit commentaire: Les oscillations de Runge sont localisées au voisinage des extrémités du domaine. Il y a par contre convergence vers la fonction au voisinage du milieu du domaine d'interpolation.

4. Du choix optimum des points de collocation

4.1 Les points de collocation de Gauss

En fait, la meilleure représentation polynômiale (c-.à-d. celle pour laquelle l'erreur est minimale) est obtenue pour un jeu de points de collocation bien connu. Depuis le milieu du XIXème sciècle, on sait que (sur l'intervalle [-1;1]), le polynôme d'interpolation optimal (de degré N donné) est celui construit sur les N+1 points de collocation x _i qui sont les racines du polynôme de Tchebychev de degré N+1.
Il s'agit des points de Gauss dont les abscisses (relatives à l'intervalle [-1;1]) sont:

4.2 Dédramatisation de l'exemple traumatisant

Si on reprend l'exemple catastrophique de l'interpolation de f(x)=1/(1+x.x), sur [-5;5], mais en réalisant cette fois l'interpolation à l'aide des points de collocation de Gauss, on obtient cette fois, pour des degrés d'interpolation n=20, 40 et 60, les erreurs suivantes:
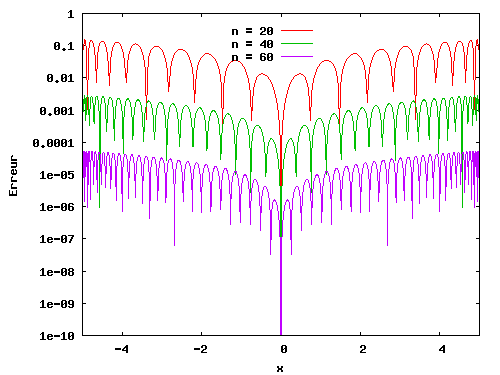
Où il est clair que tout se passe à merveille: pas d'oscillations de Runge et une représentation de la fonction d'autant meilleure (et ce, sur tout l'intervalle) que le degré polynômial est grand.