Stencils de dérivation

1. Contexte

On s'intéresse ici à un ensemble de points de collocation équidistants. On cherche à exprimer les valeurs des dérivées successives de la fonction f(x) au point de collocation x _i en fonction des valeurs de f(x) aux points de collocation voisins.
On peut évidement procéder en construisant le polynôme d'interpolation passant par les points de collocation, comme décrit dans les pages sur les polynômes de Lagrange et les matrices de dérivations sur des points équidistants. Si, par contre, on ne s'intéresse qu'à l'expression des dérivés au point milieu d'un ensemble (stentil) de points, il est plus simple d'utiliser la méthode ci-dessous.

2. Stencils de dérivations successives

2.1. Principes de la méthode

Il suffit de considérer le développement de Taylor à l'ordre p:

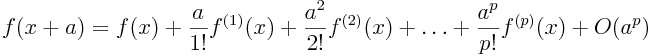
En utilisant cette formule pour a = -p.h, ..., -h, h, ..., p.h, on obtient alors un système linéaire reliant les valeurs de f(x) et ses dérivées successives en fonction des 2p valeurs entourant x:

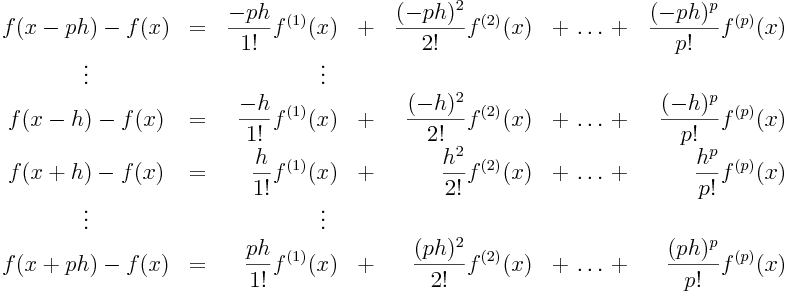
La résolution (inversion) de ce système de 2p équations à 2p inconnues permet alors d'obtenir les stencils de dérivation (c.-à-d.: les relations donnant la valeur de la dérivée k^ème au point milieu f ^(k)(x) en fonction des valeurs nodales sur l'ensemble des (2p+1) points.

Dans ce qui suit, on note f _k les valeurs de f(x) aux 2p+1 points de collocation répartis autour de x _i et espacés d'un pas h, c.-à-d. d'abscisses x _k = x _i + k.h , avec k = -p, ..., -1, 0, 1, ..., p.

2.2. Stencils de dérivation à l'ordre 2

Pour p =1, les développements de Taylor à l'ordre 2 donnent les 2 équations:

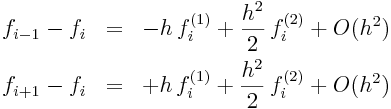
Qui permettent de relier les valeurs des dérivés première f ⁽¹⁾_i et seconde f ⁽²⁾_i au point x _i, en fonction des valeurs nodales consécutives f _i-1, f _i et f _i+1.
On obtient ainsi les stencils de dérivation (centrée) d'ordre 2 suivant:

2.3. Stencils de dérivation à l'ordre 4

Les développements de Taylor à l'ordre 4 s'écrivent:
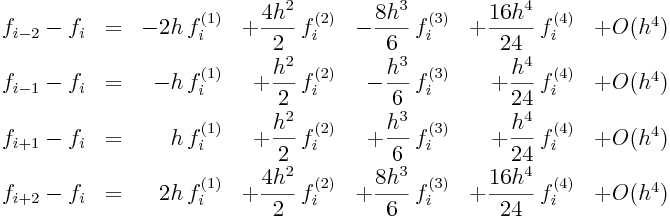
La résolution de ce système donne les stencils de dérivation suivants:

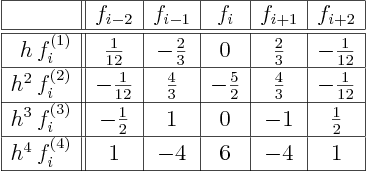
3. Quelques remarques et commentaires

• On obtiendrait ces mêmes relations en construisant (et dérivant) les polynômes de Lagrange correspondant.
• Ces stencils sont particulièrement utiles dans le cadre de la résolution d'équations différentielles avec conditions aux limites périodiques.
• Document récapitulant (fichier PDF, 2 pages, 31K) la méthode et les stencils ainsi obtenus, avec en prime les stencils d'ordre 6 et 8.