Résolution numérique d'une équation différentielle, méthode pseudospectrale (pour équation d'ordre 2 avec conditions aux limites Dirichlet, Neumann et mixtes)

Méthode pseudospectrale (Tchebychev),
sur les points de collocation de Gauss-Lobatto

1. Contexte, préambule, point de vue adopté,...

L'objectif, lorsqu'il s'agit de résoudre numériquement une équation différentielle, est d'évaluer (aussi précisément que possible) les valeurs prises par la solution (les valeurs nodales) en un certain nombre de points (les points de collocation). L'idée maîtresse sur laquelle repose cette approche est que, la solution numérique (celle obtenue aux points de collocation) tend vers la solution exacte du problème différentiel traité, l'approchant d'autant mieux que le nombre de valeurs nodales résolues est grand.
Dans le cadre de la méthode des différences finies, le degré d'approximation locale est fixe (typiquement d'ordre 2 ou 4) et la convergence, avec l'augmentation du nombre de points de collocation, vers la solution exacte est due au fait qu'une approximation de degré donné est d'autant plus précise que l'intervalle (la distance entre points de collocation voisins) sur lequel elle est construite est petit.
C'est sur ce point que diffère la méthode pseudospectrale: au lieu de figer le degré d'approximation local en chaque point de collocation et d'augmenter le nombre de ceux-ci, on construit une approximation globale (c.-à-d. basée sur l'ensemble de points de collocation). Cette approximation (polynômiale), de degré d'autant plus élevé que le nombre de point sur lequel elle est construite est grand, sera ainsi d'autant plus précise que le nombre de points de collocation employés est grand.

2. Procédure pour la résolution d'une équation différentielle avec conditions aux limites

La résolution numérique d'une équation différentielle linéaire, avec conditions aux limites, se résume à trois grandes étapes:

La discrétisation du problème, c'est à dire le choix des points de collocation sur lesquels sera approximé l'équation différentielle. De ces points découle les expressions des dérivées (en ces mêmes points) qui permettent de construire le système linéaire liant les valeurs nodales entre elles.
La prise en compte des conditions aux limites du problème: Au même tître que celles-ci complètent l'équation différentielle, leurs approximations numériques, injectées dans le système linéaire (relatif aux valeurs nodales) complètent ce dernier.
La résolution du système linéaire liant les valeurs nodales entre elles.

Pour illustrer cela, considérons l'équation différentielle d'ordre deux suivante:

Où les fonctions a₂(x), a₁(x), a₀(x) et S(x) sont données (les jeux de conditions aux limites associés, et leur traitement, est discuté plus loin).

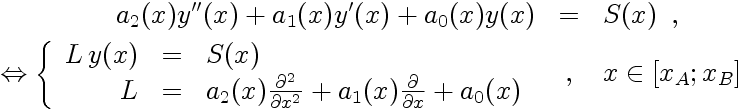
Etant donné qu'il s'agit en fin de compte de construire des approximations polynômiales de degré élevé, processus potentielement catastrophique (voir la page sur l'interpolation polynômiale), on est contraint d'utiliser des jeux de points de collocation adéquats.
On considère ici le jeu de points de collocation de Gauss-Lobatto (associés aux polynômes de Tchebychev).

Remarques:

Les points de Gauss-Lobatto (via les quadratures et les polynômes de Tchebychev sur lesquels ils sont construits) sont définis sur l'intervalle [-1;1]. Il convient donc de procéder à un changement de variable approprié pour ramener l'intervalle d'étude de [ x_A ; x_B ] à [-1;1].
Il y a d'autre jeux de points de collocation tout aussi convenables (de même qu'il existe d'autres familles de polynômes orthogonaux, ceux de Legendre par exemple, sur lesquels ces points peuvent être construits), ceux de Gauss et Gauss-Radau. L'intérêt du jeu de points de Gauss-Lobatto est que celui-ci inclue les bornes de l'intervalle.

2.1. Discrétisation du problème. Construction du système linéaire

Une fois le nombre de points de collocation (N+1), donc le degré polynômial (N) de l'approximation choisi, il faut retranscrire l'action de l'opérateur différentiel L aux valeurs nodales y_i = y(x_i), afin de construire le système matriciel L.y = S, où y est le vecteur contenant les valeurs nodales y_i , S le vecteur source dont les éléments sont les S(x_i). Les éléments de la matrice L sont donnés par: L_ij = a₂(x_i) D_ij⁽²⁾ + a₁(x_i) D_ij⁽¹⁾ + a₀(x_i) D_ij⁽⁰⁾ , où D⁽⁰⁾ est la matrice identité, et D⁽¹⁾ et D⁽²⁾ sont les matrices de dérivation première et seconde (dans l'espace physique) sur les points de Gauss-Lobatto.
Etant donné que l'expression de la matrice de dérivation première D⁽¹⁾ est connue, et que celle-ci permet de construire la matrice de dérivation seconde D⁽²⁾ (puisque, dans le cadre de développements sur les polynômes de Tchebychev, cette dernière est simplement telle que: D⁽²⁾=D⁽¹⁾.D⁽¹⁾ ), la construction de la matrice L est immédiate.

2.2. Gestion des conditions aux limites

Le système linéaire L.y = S ne rend compte que de l'équation différentielle étudiée. Or, celle-ci est assortie de conditions aux limites qu'il faut également retranscrire. Du point de vue du système linéaire, cela signifie que l'on dispose de deux contraintes complémentaires (sur les valeurs nodales extrêmes y₀ et y_N) à satisfaire. Ces contraintes, qui satisfont l'équation différentielle, sont à substituer aux expressions générales déduites ci-dessus. En clair, on remplace les équations relatives à y₀ et y_N (première et dernière lignes de la matrice L) par celles traduisant la discrétisation des conditions aux limites du problème.
Suivant la forme des conditions aux limites du problème à traiter, on distingue les types suivant:

Conditions aux limites de type Dirichlet
Les valeurs aux limites sont des données du problème: y(-1) = y_A et y(1) = y_B qui implique directement que les valeurs nodales y₀ = y_A et y_N = y_B sont connues. On peut donc aisément réécrire le système L.y = S (système (N+1)×(N+1)) sous une forme plus réduite (système (N-1)×(N-1)) L^int.y^int = S^red ne portant sur les valeurs nodales intérieures y_i, i = 1,...,N-1, où L^int est simplement l'intérieur de la matrice L et S^red est le terme source modifié par l'injection des conditions aux limites, dont les éléments sont donnés par:

L^int_ij = L_ij	pour i = 1,...,N-1 et j = 1,...,N-1
S^red_i = S_i - L_i0 y_A - L_iN y_B	pour i = 1,...,N-1

Conditions aux limites de type Neumann
Les valeurs des dérivées (premières) aux limites sont des données du problème: y'(-1) = y'_A et y'(1) = y'_B. En utilisant les relations entre les dérivés nodales y'₀ = y'_A et y'_N = y'_B et les valeurs nodales y_i (les première et dernière lignes de la relation matricielle D⁽¹⁾.y = y'), on a:

Expression des conditions aux limites Neumann aux frontières des points de Gauss-Lobatto

Qu'il faut substituer aux première et dernière lignes du système L.y = S.
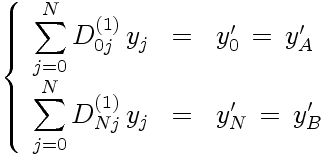
Pour être tout à fait explicite, on construit donc le système (N+1)×(N+1): L^cl.y = S^cl, dont les éléments sont:

L^cl_0j = D⁽¹⁾_0j	pour j = 0,...,N
L^cl_ij = L_ij	pour i = 1,...,N-1 et j = 0,...,N
L^cl_Nj = D⁽¹⁾_Nj	pour j = 0,...,N
S^cl₀ = y'_A
S^cl_i = S_i	pour i = 1,...,N-1
S^cl_N = y'_B

Conditions aux limites mixtes
Les valeurs aux limites et leurs dérivées sont donnéees par une relation linéaire entre elles, du type C_A y(-1) + Q_A y'(-1) = K_A et C_B y(1) + Q_B y'(1) = K_B; C_A, Q_A, K_A, C_B, Q_B et K_B étant des constantes connues.
En exprimant les dérivées nodales en fonction des valeurs nodales (comme pour le cas Neumann discuté ci-dessus), les relations aux frontières se traduisent par:

Expression des conditions aux limites mixtes aux frontières des points de Gauss-Lobatto

Ces expressions étant à substituer aux première et dernière lignes du système L.y = S.
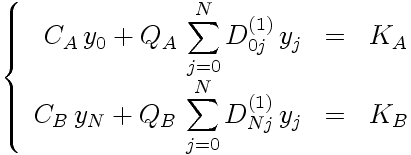
On construit donc le système (N+1)×(N+1): L^cl.y = S^cl, dont les éléments sont:

L^cl₀₀ = C_A + Q_A D⁽¹⁾₀₀
L^cl_0j = Q_A D⁽¹⁾_0j	pour j = 1,...,N
L^cl_ij = L_ij	pour i = 1,...,N-1 et j = 0,...,N
L^cl_Nj = Q_B D⁽¹⁾_Nj	pour j = 0,...,N-1
L^cl_NN = C_B + Q_B D⁽¹⁾_NN
S^cl₀ = K_A
S^cl_i = S_i	pour i = 1,...,N-1
S^cl_N = K_B

2.3. Résolution du système linéaire

Une fois le système linéaire construit, il n'y a plus qu'à le résoudre (c.-à-d. à résoudre via votre solver linéaire préféré) pour en déduire les valeurs nodales y_i recherchées.

3. Commentaires subsidiaires

Au delà d'une gestion directe des conditions aux limites, telle celle décrite ci-dessus, on peut établire une stratégie de résolution systématique de ces problèmes: En partant du système L^cl.y = S^cl ((N+1)×(N+1) éléments), on se ramène à un système réduit L^red.y = S^red ne portant que sur les valeurs nodales intérieures y_i (i = 1,...,N-1). Ces dernières, une fois obtenues, servent ensuite à reconstruire les valeurs aux limites y₀ et y_N.
Cette procédure, dite d'injection des conditions aux limites, est récapitulée ici (Fichier PDF, 3 pages, 44k)

Méthode pseudospectrale (Tchebychev), sur les points de collocation de Gauss-Lobatto