dans le cadre d'un développement sur les polynômes de Tchebychev

1. Contexte

On peut construire les matrices de dérivation aux points de collocation (Gauss,Gauss-Radau ou Gauss-Lobatto) D _N⁽¹⁾ en réalisant le double produit matriciel:

D _N⁽¹⁾ = P × D _S,N⁽¹⁾ × P ^-1

Où, rappelons-le, les éléments des matrices de dérivation spectrale D _S,N⁽¹⁾, de passage de l'espace spectral à l'espace physique P et de passage de l'espace physique à l'espace spectral P ^-1 sont facilement calculés.
En développant ces produits, et en remaniant le tout à l'aide de relations trigonométriques, on montre que les éléments des matrices D _N⁽¹⁾ peuvent être construit en bien moins d'opérations, et de plus uniquement à partir des abscisses du jeu de points de collocation considéré.

2. Expressions des matrices de dérivation première dans l'espace physique

2.1. Sur les points de collocation de Gauss

Pour le jeu de points de collocation de Gauss:
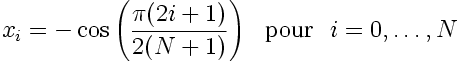
Les éléments de la matrice de dérivation première D _N⁽¹⁾ sont:

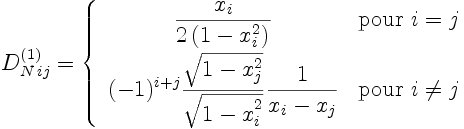
2.2. Sur les points de collocation de Gauss-Radau

Pour le jeu de points de collocation de Gauss-Radau:
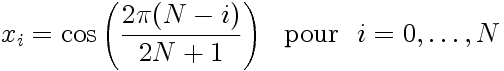
Les éléments de la matrice de dérivation première D _N⁽¹⁾ sont:

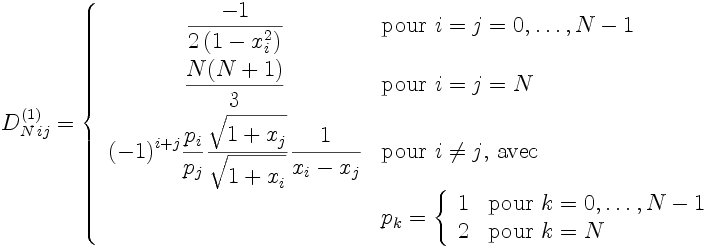
2.3. Sur les points de collocation de Gauss-Lobatto

Pour le jeu de points de collocation de Gauss-Lobatto:
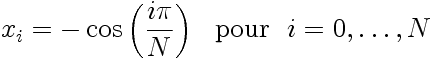
Les éléments de la matrice de dérivation première D _N⁽¹⁾ sont:

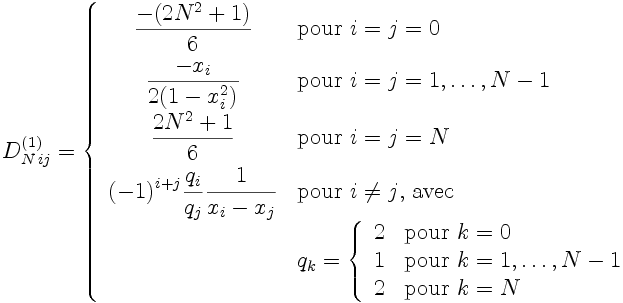
3. Dérivées d'ordre supérieur

Les matrices de dérivation d'ordre k, D _N^(k), s'obtiennent simplement en tant que produits (k fois) de la matrice de dérivation première D _N⁽¹⁾ du jeu de points de collocation considéré.

Petit formulaire (fichier PDF, 2 pages, 34k) récapitulant l'expression de ces matrices.