via le développement sur les polynômes de Tchebychev

1. Dérivée physique et dérivée spectrale

Le polynôme d'interpolation de degré N (construit sur N+1 points de collocation x _i de l'intervalle [-1;1]) f_N(x) , d'une fonction f(x), a pour développement sur les polynômes de Tchebychev: Où les coefficients spectraux c_k sont complètement déterminés (voir les pages sur les polynômes de Tchebychev et matrices de passage associées).

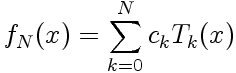
Pour évaluer la dérivée de f(x), Il faut calculer celle de f_N(x). Lorsqu'il s'agit d'évaluer cette dérivée aux points de collocation, on peut écrire les relations entre dérivées nodales y_i⁽¹⁾ = f_N⁽¹⁾(x _i) et valeurs nodales y_i = f_N(x _i) sous la forme d'un système linéaire D _N⁽¹⁾×y⁽¹⁾ = y (ainsi qu'explicité au sujet de la dérivation des polynômes d'interpolation de Lagrange). De ce point de vue, on qualifie la matrice D _N⁽¹⁾ de matrice de dérivation dans l'espace physique, puisqu'elle exprime le lien entre les valeurs aux points de collocation et les valeurs des dérivées en ces mêmes points.
On peut adopter un point de vue complémentaire: La dérivé peut, tout comme le polynôme d'interpolation, être considérée du point de vue de son développement sur les polynômes de Tchebychev. Il existe ainsi une relation entre les coefficients spectraux de chacun de ces développements qui se met sous la forme d'un système linéaire: D _S,N⁽¹⁾×c⁽¹⁾ = c, où c est le vecteur des coefficients spectraux c_k de f_N(x), c⁽¹⁾ le vecteur des coefficients spectraux c_k⁽¹⁾ de f_N⁽¹⁾(x) et D _S,N⁽¹⁾ la matrice de dérivation dans l'espace spectral.

2. Matrice de dérivation spectrale

La dérivée de f_N(x) est égale à celle de son développement. Or les dérivées des polynômes de Tchebychev sont telles que:
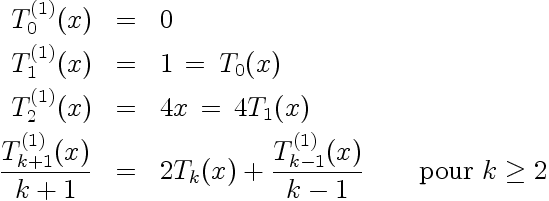
A l'aide de ces relations, on montre que les éléments de la matrice de dérivation spectrale D _S,N⁽¹⁾ sont: En d'autres termes, la matrice D _S,N⁽¹⁾ est triangulaire supérieure, à diagonale nulle, et bien creuse (la moitié des éléments de la partie triangulaire sont nuls).

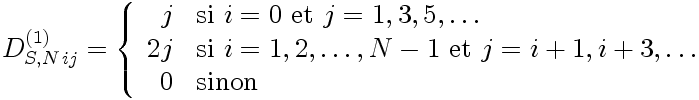
3. Liens entre matrices de dérivation physique et spectrale

En partant des relations (via les matrices de passage P et son inverse P ^-1 ) entre valeurs nodales et coefficients spectraux: P×c = y et P ^-1×y = c, qui par ailleurs lient également valeurs nodales et coefficients spectraux de la dérivée: P×c⁽¹⁾ = y⁽¹⁾ et P ^-1×y⁽¹⁾ = c⁽¹⁾, et en tenant compte des relations de dérivation: D _N⁽¹⁾×y⁽¹⁾ = y et D _S,N⁽¹⁾×c⁽¹⁾ = c, on montre que:

D _N⁽¹⁾ = P × D _S,N⁽¹⁾ × P ^-1

Relation particulièrement utile puisqu'elle permet de construire la matrice de dérivation physique D _N⁽¹⁾ à partir des matrices de passage P et P ^-1, et de la matrice de dérivation spectrale D _S,N⁽¹⁾.
Il existe d'autre part des procédures pour construire cette matrice de dérivation plus directement.

4. Dérivées d'ordres supérieurs

En suivant des raisonnements similaires à ceux donnés ci-dessus, on montre que les matrices de dérivation (aussi bien spectrale que physique) d'ordre n sont simplement égales au produit de la matrice de dérivation première par elle-même. En clair, D _S,N⁽²⁾ = D _S,N⁽¹⁾ × D _S,N⁽¹⁾, D _N⁽²⁾ = D _N⁽¹⁾ × D _N⁽¹⁾, D _S,N⁽³⁾ = D _S,N⁽¹⁾ × D _S,N⁽²⁾, D _N⁽³⁾ = D _N⁽¹⁾ × D _N⁽²⁾, ...