Formules de Newton-Cotes
1. Contexte
On souhaite évaluer l'intégrale d'une fonction f(x) sur un intervalle [A,B] = [x 0,x m]. L'intervalle est subdivisé en m sous-intervalles de taille h et les valeurs y i = f(x i) aux points x i = x 0+i×h , i = 0, ... , m sont connues.Etant donné que l'on peut, á l'aide de n points, construire un polynôme de degré (n-1) et que l'integrale de ce dernier (sur [x 0,x n]) peut s'écrire sous la forme d'une somme pondérée des y i correspondants, l'évaluation de l'intégrale de f(x) sur [A,B] se résume de même à une somme pondérée des y i.
2. Formules de Newton-Cotes
En écrivant que l'intégrale de f(x) sur [x 0,x n] peut s'exprimer comme une combinaison linéaire des y i , on arrive à:
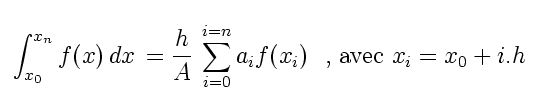
|
Les valeurs de A et des coefficients ai sont alors:
| Nom usuel de la formule | n | A | a0 | a1 | a2 | a3 | a4 | a5 | a6 |
| Trapèzes | 1 | 2 | 1 | 1 | |||||
| Simpson | 2 | 3 | 1 | 4 | 1 | ||||
| "Newton-Cotes 3" | 3 | 8 | 3 | 9 | 9 | 3 | |||
| Boole-Villarceau | 4 | 45 | 14 | 64 | 24 | 64 | 14 | ||
| Hardy | 6 | 140 | 41 | 216 | 27 | 272 | 27 | 216 | 41 |
Remarque:
- La méthode des trapèzes est exacte pour un polynôme
de degré 1; celle de Simpson est exacte pour un polynôme
de degré 3; celle de Boole-Villarceau est exacte pour un
polynôme de degré 5 ...
En fait, pour n pair, la formule de Newton-Cotes est exacte pour un polynôme de degré n+1, tandis que pour n impair, la formule est exacte pour un polynôme de degré n. C'est pourquoi on emploie quasi-exclusivement les formules associées aux stencils pour lesquels n est pair.
3. Aspects pratiques
Les formules de Newton-Cotes souffrent du même problèmes que les polynômes d'interpolation sur points équidistants: une mauvaise représentation de la fonction f(x) sur les bords du domaine.En pratique, on utilise ainsi un stencil composé de peu de points (par exemple 3, pour la formule de Simpson) et le calcul de l'integrale de f(x) sur [x 0,x m] est ramené à la somme de celles, évaluées par la formule de Simpson, calculées sur [x 0,x 2], [x 2,x 4],...
3.1 Un exemple pour illuster le tout
Soit à déterminer l'intégrale de f(x) = cos(pi.x).exp(x) sur [-1;1]:
![Fonction f(x)=cos(pi.x).exp(x) sur [-1;1] Fonction f(x)=cos(pi.x).exp(x)](exemple1_fonction.png)
|
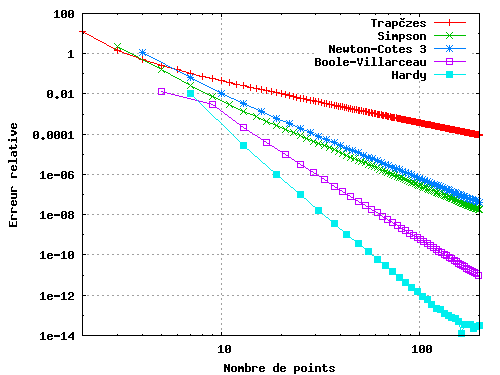
f(x) étant connue, elle peut être évaluée en n'importe quelle valeur de x, et donc n'importe quel jeux de x i sur lesquels utiliser les formules de Newton-Cotes. En augmentant le nombre de points (et donc le nombre de stencils associés à la méthode employée), on tends vers la solution exacte, ainsi que l'illustre la figure suivante:
|
Où on retrouve les faits suivants:
- L'odre des méthodes est d'autant plus grand que le stencil associé est de degré élevé
- Les méthodes de Simpson et "Newton-Cotes 3" sont de même ordre (c.f. remarque plus haut).
3.2 Autres commentaires et remarques
Lorsqu'il s'agit de calculer l'intégrale d'une fonction f(x) connue (telle que celle de l'exemple ci-dessus), choisir les x i (et calculer les f(x i) correspondants) ne pose pas de problème particulier.Il arrive toutefois souvent que l'on ne dispose pas de la forme de la fonction f(x), par exemple lorsque les valeurs aux points x i sont issues d'un calcul numérique, et que l'on ne puisse donc pas "raffiner" l'évaluation de l'intégrale en augmentant le nombre de points; la seule alternative repose alors sur l'emploi de formules d'ordres plus élevé. Se pose alors le problème pratique suivant: le nombre de points (m+1) sur lequel calculer l'intégrale est fixe, tout comme ceux des stencils associés aux diverses formules de Newton-Cotes (par ex.: la formule de Boole-Villarceau, basée sur un stencil de 5 points, ne peut s'appliquer que sur des paquets de 5,9,11,... (c.-à-d.: 1+4.n, n=1,2,...) points). On se trouve alors obligé d'ultiliser la formule choisie sur autant de points que possible, puis d'utiliser une formule plus limitée sur l'intervalle restant.