Intégration numérique sur un ensemble de points
1. Méthode générale
On souhaite évaluer l'intégrale d'une fonction f(x) sur un intervalle [A,B] = [x 0,x m], à l'aide des valeurs y i = f(x i). Sachant que l'on peut, à l'aide de n points, approcher f(x) par un polynôme de degré (n-1) dont l'intégrale est donnée par une somme pondérée des y i:
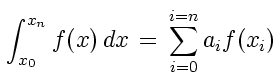
|
Il reste alors a déterminer les coefficients a i, ce qui revient à s'assurer qu'ils sont tels qu'il y ait égalité stricte entre l'intégrale et le somme lorsque f(x) est remplacée par un monôme de degré inférieur ou égal à n.
On obtient alors le système linéaire (de type Vandermonde) suivant:
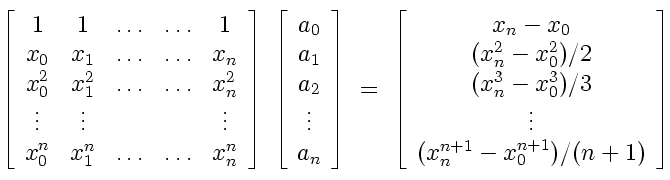
|
Qu'il suffit de résoudre pour déterminer les valeurs des coefficients a i.
Remarques:
- Pour n=1, on retrouve évidement la formule des trapèzes. De même, dans le cas de points équidistants x i = x 0+i.h , on retrouve les formules de Newton-Cotes.
- Comme toujours lorsqu'il s'agit de représenter une fonction f(x) inconnue par un polynôme, il n'est généralement pas très bon d'utiliser des polynômes de degré très élevés (voir la page traitant de l'interpolation). Disposant d'un grand nombre de points, il est préférable de subdiviser l'intervalle en sous-intervalles de quelques points sur lesquels seront appliquées les formules obtenues à partir des rélations données ci-dessus. D'où l'intérêt de déterminer la dépendence des a i en fonction des x i (en d'autres termes, résoudre le système linéaire à la main).
2. Expression des coefficients a i
Petit rappel: La solution du système linéaire A.x = y (où le vecteur y et la matrice A sont connus) est telle que x = A-1.y (à condition, bien évidement, que A soit inversible, et c'est ici le cas). Il "suffit" donc d'inverser la matrice et d'effectuer le produit avec le second membre.2.1 Coefficients pour n = 2
Après quelques calculs, on arrive à:
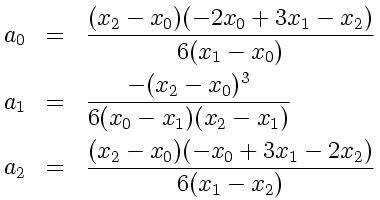
|
2.2 Coefficients pour n = 3
Après d'autres calculs, un peu plus fastidieux, on arrive à:
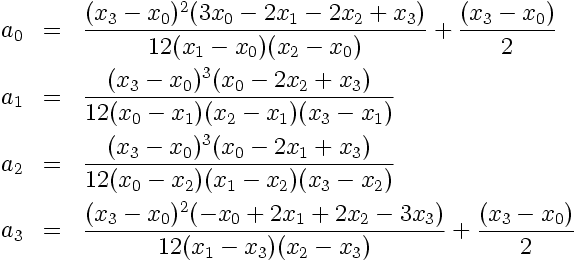
|
2.3 Coefficients pour n = 4
Après une bonne dose de calculs supplémentaires, on obtient:
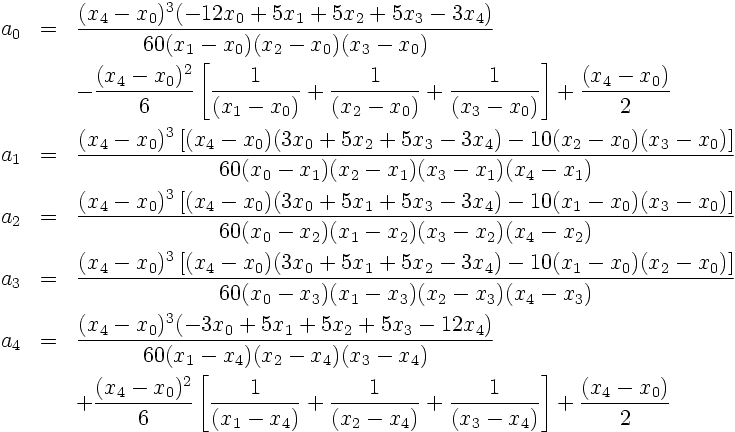
|
3. Remarques et commentaires
Ces formules sont valables pour un jeu quelconque de points x i, à la seule condition (est-il nécessaire de le préciser?) qu'ils soient tous distincts. On peut ainsi les employer pour calculer l'intégrale entre deux points x j et x k, en s'appuyant éventuellement sur des points en dehors de l'intervalle [x j, x k].Exemple: On connait les valeurs y i prises en 4 points x 0, x 1, x 2 et x 3 d'une fonction (inconnue) dont on souhaite évaluer l'intégralle de x 1 à x 2. On peut, en réarrangeant les données (c.-à-d. en posant X 0 = x 1, X 1 = x 0, X 2 = x 3, X 3 = x 2 et sans oublier d'également permuter les y i: Y 0 = y 1, Y 1 = y 0, Y 2 = y 3, Y 3 = y 2) utiliser la formule sur 4 points (n=3) donnée ci-dessus.