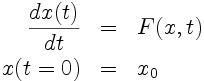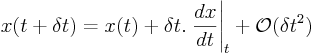Définition et exemple illustratif

1. Contexte

Dans la mesure où un schéma d'intégration temporelle revient à approximer au mieux la dérivée d'une fonction (sur l'intervalle défini par deux instants successifs) et donc en fait d'approximer au mieux le développement de Taylor celle-ci, l'erreur due à une méthode d'intégration est directement liée à la tronquature correspondante.
Ainsi l'approximation d'Euler (explicite, dans l'exemple qui suit) de l'équation différentielle: ordinaire: s'écrit: L'erreur comise à chaque itération peut être estimée en via le développement de Taylor: qui indique qu'à chaque itération on introduit une erreur proportionelle au carré du pas de temps. Ces erreurs vont s'accumuler au fils des itérations temporelles, ce qui au final fait remonter l'erreur d'un ordre de grandeur lorsque l'on évalue l'erreur totale à un instant quelconque.

2. Exemple illustratif

Rien ne vaut un exemple pour illustrer tout cela.
Soit donc l'équation différentielle suivante: Dont la solution est: Disposant de la solution analytique, on peut étudier la convergence vers celle-ci des solutions numériques obtenues par différents schémas temporels: On intègre, par plusieurs méthodes (Euler explicite et Runge-Kutta 2,3 et 4) et pour plusieurs pas de temps dt (variant de 2 à 0.0001) cette équation et on regarde l'écart (relatif, c.-à-d. la valeur absolue de la différence entre valeurs numérique et analytique, divivée par la valeur analytique) au temps t=4 entre solutions numérique et analytique. 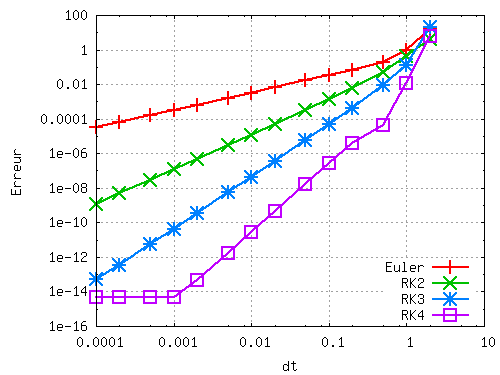On obtient alors les écarts relatifs suivant: Graphe qui illustre les points suivants:

• Pour un pas de temps suffisament petit (ici lorsque dt est plus petit que 0,2) on observe la décroissance attendue du schéma employé: pour la méthode d'Euler, lorsqu'on diminue le pas de temps d'une décade, l'erreur dimine également d'une décade, tandis que pour cette même diminution du pas de temps, l'erreur pour la méthode Runge-Kutta 2 décroit de 2 décades, celle de Runge-Kutta 3 de 3 décades et celle de Runge-Kutta 4 de 4 décades.
• Le comportement de décroissance de l'erreur tel qu'attendu par l'ordre (théorique) de la méthode n'a lieu qu'à partir d'un pas de temps dt suffisament petit.
• Les calculs étant réalisés à une précision donnée, on atteint une saturation (typiquement d'un ordre de grandeur suppérieur à l'epsilon machine) pour un pas de temps suffisament petit. Ce qui s'observe dans l'exemple ci-dessus avec la méthode de Runge-Kutta 4 pour un dt inférieur à 0.001; que l'on verrait pour les autres méthodes si on avait poursuivit l'étude avec des dt inférieurs.

3. Commentaires subsidiaires

• Le fait que la décroissance de l'erreur ne soit telle qu'attendue qu'à partir d'un pas de temps dt suffisament est liée au fait que l'erreur de troncature du développement de Taylor n'est proportionnel à l'ordre du premier terme néglig;é que dans la mesure d'un dt suffisament petit.
• En pratique, on ne dispose pas de la solution analytique et on ne peut déterminer l'erreur effectivement comise. Il est impératif, pour chaque cas de figure, de réaliser des calculs pour plusieurs valeurs de dt afin de s'assurer de la bonne convergence de la résolution et de se faire une idée de la précision effective de la solution nuérique.
• Les méthodes d'ordre élevé sont plus précises, mais plus lourdes à mettre en oeuvre. Dans la pratique, il faut considérer le coût total, c'est à dire le temps de calcul nécessaire pour produire des résultats d'une précision donné. On s'appercoit alors souvent que les méthodes d'ordre élevés sont très avantageuses.