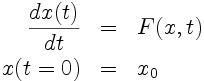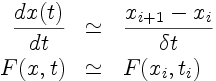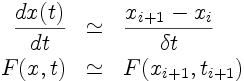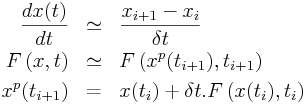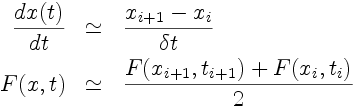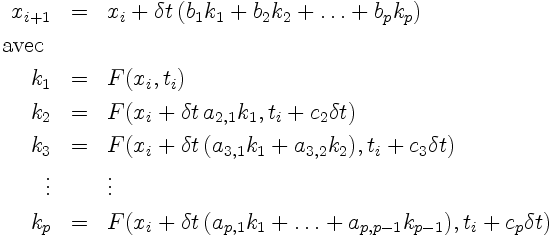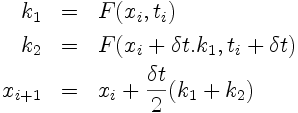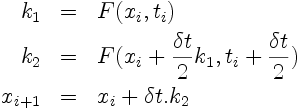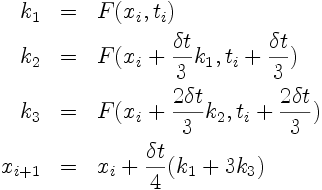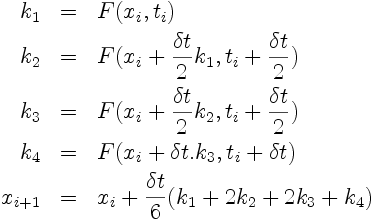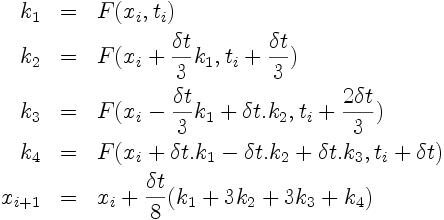Schémas à pas unique
(Euler, Crank-Nicholson, Runge-Kutta)
1. Contexte
On recherche la solution de l'équation différentielle
ordinaire:
Où l'expression du second membre F(x,t) et
la valeur de la condition initiale x(t = 0) sont données.
On souhaite de plus se restreindre à des schémas
d'intégration temporelle à pas unique,
c.-à-d. permettant de determiner la solution
à l'instant t
i+1 à partir de celle
obtenue à l'instant précédent.
Pour alléger la notation, x
k
représente, dans ce qui suit, x(t
k).
2. Schémas d'Euler
Ces schémas sont d'une précision d'ordre 1 en temps.
2.1. Schéma d'Euler explicite
Principe:
L'équation est évaluée à l'instant
t
i.
La dérivée temporelle est déduite
de la dérivée du polynôme d'interpolation
basé sur x
i et x
i+1.
2.2. Schéma d'Euler implicite
Aussi connu sous l'appellation
Euler retardé (d'ordre 1)
Principe:
L'équation est évaluée à l'instant
t
i+1.
La dérivée temporelle est déduite
de la dérivée du polynôme d'interpolation
basé sur x
i et x
i+1.
3. Schéma prédicteur-correcteur de Matsuno
Principe: En combinant les schémas d'Euler explicite et implicite
on décompose la résolution en deux étapes, on utilise
dans un premier temps (la phase prédicteur du schéma) le
schéma Euler explicite pour une première évaluation de
x
i+1, x
pi+1; cette derniè est ensuite
utilisée dans un deuxième temps (la phase correcteur)
pour évaluer le second membre
F
p(x
pi+1,t
i+1) d'une
résolution à la Euler implicite.
Ce scémas est d'une précision d'ordre 1 en temps.
4. Schéma de Crank-Nicholson
Principe:
L'équation est évaluée à l'instant
intermédiaire t
i+1/2 =
(t
i + t
i+1)/2.
La dérivée temporelle est déduite
de la dérivée du polynôme d'interpolation
basé sur x
i et x
i+1.
Le second membre est déduit du polynôme
d'interpolation basé sur
F(x
i,t
i) et
F(x
i+1,t
i+1).
Ce schéma est implicite,
puisque F(x
i+1,t
i+1) intervient
dans la détermination de x
i+1,
et est d'une précision d'ordre 2 en temps.
5. Les schémas de Runge-Kutta
5.1. Principes de l'approche
Les schémas de Runge-Kutta d'ordre p
sont de la forme:
où les coefficients a
ij, b
i et c
i
sont déterminés afin que l'expression
x
i+1 = x
i + ... du schéma
coïncide avec le développement de Taylor (à l'ordre p) de
x
i+1.
Ces schémas sont explicites et de précision d'ordre p
en temps.
Remarque:
La détermination des m coefficients mène à un
système de n équation, où n < m. On peut
alors fixer arbitrairement les valeurs des (m-n) coefficients
excédentaires. Conséquement, il n'y a pas
de formule unique (à un ordre p donné), mais une infinité
de possibilités. Toutefois, des considérations de
stabilité et minimisation du nombre d'opérations
intermédiaires conduisent aux schémas usuels
donnés ci-dessous.
5.2. Schéma de Runge-Kutta 2
Schémas RK2 "classique"
(parfois aussi appelée
schéma d'Euler modifié):
Variante (aussi connue sous l'appellation
méthode de la tangente améliorée,
ou encore
schéma de Heun):
5.3. Schéma de Runge-Kutta 3
5.4. Schémas de Runge-Kutta 4
Le plus classique:
Une variante: