Généralités

1. Intégration d'équations différentielles ordinaires

1.1. Introduction

Une équation différentielle ordinaire (d'ordre 1) est de la forme: Où l'expression du second membre F(x,t) et la valeur de la condition initiale x(t = 0) sont données.
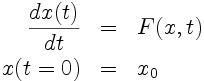
Dans les cas les plus simples, x(t) représente une seule variable. Plus généralement (lorsqu'il s'agit d'un système d'équations différentielles couplant plusieurs variables), x(t) est un vecteur regroupant les inconnues.

La (les) solution(s) x(t) s'étend(ent) a priori sur l'intervalle semi-infini des t positifs. Conséquement, la procédure de résolution numérique de l'équation n'est pas la détermination d'une solution approchée "en bloc" sur un intervalle (straégie parfaitement adaptée pour la résolution d'équations différentielles avec conditions aux limites); on cherche plutôt à "suivre" l'évolution de x(t), depuis sa condition initiale x(t = 0) jusqu'à une valeur de t donnée (bien que par ailleurs parfaitement arbitraire).

Typiquement, ce type de problème aux conditions initiales concerne l'évolution temporelle d'un système; on désigne donc les procédures de résolution de schémas d'intégration temporelle ou, d'une façon plus imagée, de procédure de marche dans le temps (de "time marching" en anglais).
Les principes de bases de cette approche sont simplement de subdiviser le temps t en instants successifs t_i (le plus souvent régulièrement espacés; c.-à-d. tels que t_i = i.h ) et de construire une approximation numérique reliant la solution (encore indéterminée) à l'instant t_n : x(t_n) à celle(s) du (ou des) instant(s) précédent(s) (connus).
Ainsi, connaissant la condition initiale x(t₀), on construit x(t₁), qui sert ensuite à déterminer x(t₂), qui permettera de calculer x(t₃), ...

Bien évidement, un schémas d'intégration temporelle employé sera plus ou précis et fiable selon le(s) degré(s) d'approximation(s) qu'il inclue. Entre autres critères, on distingue en particulier l'ordre des différements schémas qui donne (au moins théoriquement) le taux de convergence, en fonction du pas de temps (l'écart entre les instants successifs calculés). Voir la page sur l'ordre des schémas temporels pour plus de détails sur ce sujet.

1.2. Construction de systèmes équivalents d'ordre 1

Lorsqu'une équation différentielle ordinaire (ou un système d'équations différentielles ordinaires) contient des dérivées d'ordre supérieur (à 1), il est toujours possible de construire un système équivalent d'ordre 1 en introduisant des variables intermédiaires. Ces variables intermédiaires sont simplement les dérivés successives des variables initiales.
Exemple: L'équation différentielle d'ordre 2:
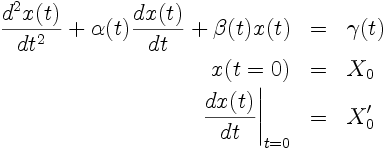
devient, en posant y(t) = x'(t), le système équivalent (de 2 équations d'ordre 1):

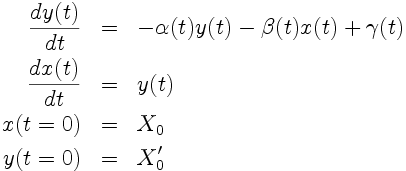
1.3. Les schémas d'intégration temporelle

On dispose d'un large éventail de possibilités pour discrétiser les termes (dx/dt et F(x,t)) de l'équation différentielle. Suivant les approches, on distingue les deux "familles" de schémas d'intégration temporelle suivantes:

• Schémas à pas unique: l'état du système à l'instant t_n+1 est construit à partir de son état antérieur t_n.
• Schémas à pas multiples: l'état du système à l'instant t_n+1 est construit à partir de N états antérieurs t_n, t_n-1, ..., t_n-N.

On distingue de plus, suivant la façon dont est discrétisé le second membre F(x,t), les formulations suivantes:

• Méthodes explicites: La valeur du second membre à l'instant t_n+1 : F(x(t_n+1),t_n+1) n'intervient pas dans la détermination de x(t_n+1). On construit ainsi des schémas qui sont de la forme x(t_n+1) = S, ou S ne contient que des termes connus (x(t_n), F(x(t_n),t_n), ...).
• Méthodes implicites: La valeur du second membre à l'instant t_n+1 : F(x(t_n+1),t_n+1) intervient dans la détermination de x(t_n+1). Ces schémas mènent à une équation liant x(t_n+1) et F(x(t_n+1),t_n+1); équation qu'il faudra résoudre pour déterminer x(t_n+1). Cette dernière étape peut s'avérer particulièrement délicate, en particulier lorsque F(x,t) est non linéaire (par rapport à x).
• Méthodes semi-implicites: Certains termes de F(x,t) sont construit suivant une formulation implicite, d'autres suivant une formulation explicite. Généralement, les termes linéaires sont implicités et les termes non linéaires sont explicités.

Description de quelques schémas à pas unique (Euler, Crank-Nicholson, Runge-Kutta), schémas à pas multiples (Euler retardé, Adams-Bashforth, Adams-Moulton).

2. Intégration d'équations différentielles aux dérivées partielles

Ce qui est écrit ci-dessus s'applique également aux équations aux dérivées partielles. Pour celles-ci, le second membre contient des dérivées partielles par rapport à des paramètres autre que t (typiquement des des dérivées par rapport aux variables d'espace). Ce qui signifie que, une fois la discrétisation temporelle effectuée, il faudra résoudre un système différentiel (aux conditions aux limites) pour déterminer l'état du système à l'instant t_n+1, résolution à renouveller à chaque itération temporelle.