Schémas à pas multiples (Euler retardé, Adams-Bashforth, Adams-Moulton)
1. Contexte
On recherche la solution de l'équation différentielle ordinaire:
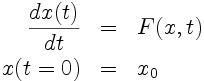
|
On s'intéresse ici aux schémas d'intégration temporelle à pas multiples, c.-à-d. permettant de determiner la solution à l'instant ti+1 à partir de celles obtenues aux instants antérieurs.
Pour alléger la notation, xk représente, dans ce qui suit, x(tk); de même, Fk signifie F(x(tk),tk).
2. Schémas d'Euler retardé
Principe: L'équation est évaluée à l'instant ti+1. La dérivée temporelle est déduite de la dérivée du polynôme d'interpolation basé sur xi+1, xi, xi-1, ...
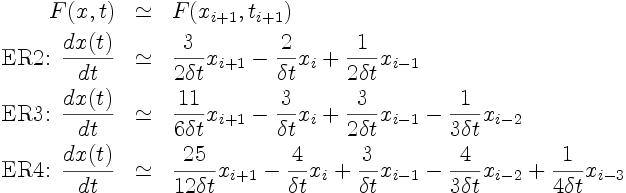
|
Ces schémas sont implicites.
Remarque:
En se limitant à l'ordre 1, on retrouve le schéma (à pas unique) d'Euler implicite.
En se limitant à l'ordre 1, on retrouve le schéma (à pas unique) d'Euler implicite.
3. Schémas d'Adams-Bashforth
Principe: Le développement de Taylor de xi+1 permet d'exprimer xi+1 en fonction de xi et de ses dérivées successives. Or, d'après l'équation différentielle (que l'on cherche à résoudre), x'i = Fi, x"i = F'i, ..., ce qui mène à une expression donnant xi+1 en fonction de xi, Fi et ses dérivées successives F'i, F"i,... Ces dernières sont évaluées à l'aide du polynôme d'interpolation (et ses dérivées) basé sur les valeurs Fi, Fi-1, ...On obtient ainsi les schémas suivants:
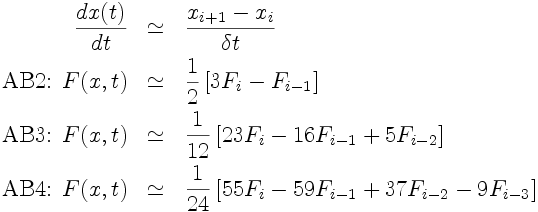
|
Ces schémas sont explicites.
Remarque:
A l'ordre 1, on retrouve le schéma (à pas unique) d'Euler explicite.
Ces schémas sont conditionnellement stable; il est impératif d'utiliser un pas de temps suffisamment petit si on veut éviter d'obtenir une solution qui diverge (c.-à-d. qui s'éloigne indéfiniment de la solution de l'équation différentielle).
A l'ordre 1, on retrouve le schéma (à pas unique) d'Euler explicite.
Ces schémas sont conditionnellement stable; il est impératif d'utiliser un pas de temps suffisamment petit si on veut éviter d'obtenir une solution qui diverge (c.-à-d. qui s'éloigne indéfiniment de la solution de l'équation différentielle).
4. Schémas d'Adams-Moulton
Principe: On procède de même que pour les schémas d'Adams-Bashforth, mais à partir du développement de Taylor "arrière" de xi+1-1 permettant d'exprimer xi en fonction de xi+1, x'i+1, x"i+1, etc.On aboutit aux expressions suivantes:
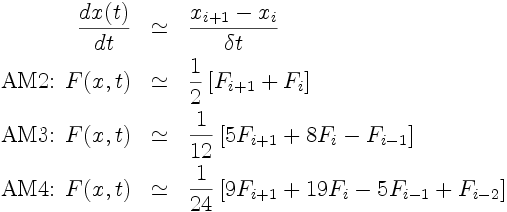
|
Ces schémas sont implicites.
Remarque:
Le schémas AM2 s'avère être à pas unique; on retrouve d'ailleurs là l'expression du schéma de Crank-Nicholson.
Le schémas AM2 s'avère être à pas unique; on retrouve d'ailleurs là l'expression du schéma de Crank-Nicholson.
5. Schémas Prédicteurs-Correcteurs
On peut combiner des schémas afin d'utiliser au mieux le(s) avantage(s) des uns et des autres. Un exemple classique est de combiner les schémas d'Adams-Bashforth et Adams-Moulton afin d'éviter la délicate résolution d'un système implicite de ces derniers. On emploie dans un premier temps un schéma (d'ordre N) d'Adams-Bashforth pour calculer une première approximation (phase prédicteur) de xi+1, xpi+1. C'est cette prédiction qui est ensuite injectée dans les calculs des termes du second membre (les Fk) d'un schémas d'Adams-Moulton.On obtient ainsi par exemple en combinant AB2 et AM2:
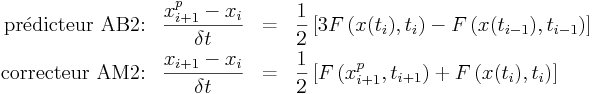
|
Remarque:
En combinant AB1 et AM1 (c.à-d. Euler explicite et implicite) on obtient ainsi le schéma de Matsuno.
Il arrive également que l'on construise des combinaisons prédicteur-correcteur avec des schémas d'ordres différents (typiquement en choisissant d'utiliser un schéma d'ordre inférieur pour la partie prédiction) par exemple AB2-AM3.
En combinant AB1 et AM1 (c.à-d. Euler explicite et implicite) on obtient ainsi le schéma de Matsuno.
Il arrive également que l'on construise des combinaisons prédicteur-correcteur avec des schémas d'ordres différents (typiquement en choisissant d'utiliser un schéma d'ordre inférieur pour la partie prédiction) par exemple AB2-AM3.
6. Aspects pratiques
Le fait que ces schémas reposent sur la connaissance de valeurs (de x et/ou F) à plusieurs instants antérieurs pose généralement un problème lors de l'initialisation de la procédure d'intégration temporelle. Par exemple, pour illustrer ce problème, si l'on dispose de la condition initiale x0 (et conséquement de F0 ) et que l'on souhaite utiliser le schémas AB2, alors x1 s'exprime en fonction de x0 , F0 et F-1 ; c'est (évidement) ce dernier terme qui pose problème (puisqu'il dépend de x-1 , quantité inconnue). Pour remédier à cette difficultée d'initialisation, il faut avoir recours à l'un des stratagèmes suivant:- Inventer (où plutôt extrapoler) les valeurs manquantes; démarche quelque peu hasardeuse, mais justifiable dans certains contextes, par exemple lorsqu'il s'agit d'étudier l'évolution temporelle d'un système physique initialement au repos.
- Utiliser une(des) variante(s) d'ordre(s) inférieur(s) du schéma sur la(les) première(s) itération(s). Pour l'exemple ci-dessus, on calculerait ainsi x1 à l'aide du schéma AB1 (c.-à-d. Euler explicite à pas unique). L'intérêt pratique de cet approche découle du fait que si on a déjà implémenté une procédure de résolution associée à un schémas d'ordre k, adapter/modifier cette dernière pour construire une procédure d'ordre inférieur ne demande finalement que peu de temps (et de sueur).
- Utiliser un schémas à pas unique (de même précision temporelle) pour calculer la(les) première(s) valeurs de x. Formellement, c'est l'option la plus sensée; malheureusement, c'est la plus lourde à mettre en œuvre puisqu'il faut implémenter deux solvers (aux fonctionnements assez distincts).